 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
提问人:网友shuxinmiao
发布时间:2022-06-23
[主观题]
证明:如果A是n级斜对称实矩阵,那么eA是正交矩阵。
 简答题官方参考答案
(由简答题聘请的专业题库老师提供的解答)
简答题官方参考答案
(由简答题聘请的专业题库老师提供的解答)
查看官方参考答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
 简答题官方参考答案
(由简答题聘请的专业题库老师提供的解答)
简答题官方参考答案
(由简答题聘请的专业题库老师提供的解答)
 更多“证明:如果A是n级斜对称实矩阵,那么eA是正交矩阵。”相关的问题
更多“证明:如果A是n级斜对称实矩阵,那么eA是正交矩阵。”相关的问题
设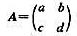 是一个实矩阵且ad-bc=1。证明:
是一个实矩阵且ad-bc=1。证明:
(i)如果|trA|>2,那么存在可逆实矩阵T,使得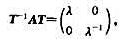 这里λ∈R且λ≠0,1,-1;
这里λ∈R且λ≠0,1,-1;
(ii)如果|trA|=2且A≠±1,那么存在可逆实矩阵T,使得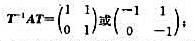
(iii)如果|trA|<2,则存在可逆实矩阵T及θ∈R,使得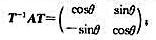
n维欧氏空间V的一个线性变换σ说是反对称的,如果对于任意向量a,β∈V。
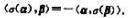 证明:
证明:
(i)反对称变换关于V的任意规范正交基的矩阵都是反对称的实矩阵(满足条件AT=-A的矩阵叫作反对称矩阵);
(ii)反之,如果线性变换σ关于V的某一规范正交基的矩阵是反对称的,那么σ一定是反对称线性变换;
(iii)反对称实矩阵的特征根或都是零,或者是纯虚数。
(1)设A、C分别为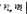 阶实对称矩阵,B是
阶实对称矩阵,B是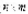 实矩阵,
实矩阵,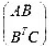
是正定矩阵(实)。证明:
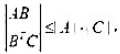 等号当且仅当B=0时成立.
等号当且仅当B=0时成立.
(2)设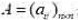 是n阶实矩阵,
是n阶实矩阵,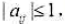
求证:
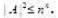

 警告:系统检测到您的账号存在安全风险
警告:系统检测到您的账号存在安全风险
为了保护您的账号安全,请在“简答题”公众号进行验证,点击“官网服务”-“账号验证”后输入验证码“”完成验证,验证成功后方可继续查看答案!
